Integration of prior information in Kaplan Meier estimator using Bayesian approach

Article Sidebar

AJB (20-007) Hamimes et al
Published: Dec 30, 2020
DOI: https://doi.org/10.57056/ajb.v1i2.30
Keywords:
Bayesian approach, nonparametric survival, Kaplan Meier, Bayesian estimator

Main Article Content

Ahmed Hamimes

Abstract

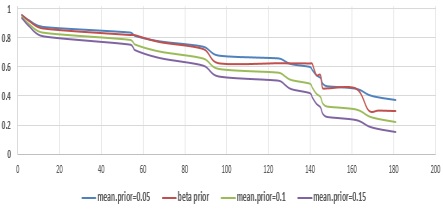
As part of this contribution, we will illustrate the effectiveness of the Bayesian approach in estimating durations; we suggest a new definition of the Kaplan Meier Bayesian estimator based on a stochastic approximation under an informative prior. For this reason, based on the lognormal distribution, we have unconjugated a priori distributions. This method of processing makes it possible to assume that the use of the a priori data with the various suggested methods is sensitive to the choices of the parameters added.

Article Details

How to Cite
Hamimes, A. (2020). Integration of prior information in Kaplan Meier estimator using Bayesian approach. Algerian Journal of Biosciences, 1(2), 076–082. https://doi.org/10.57056/ajb.v1i2.30
Issue
Vol. 1 No. 2 (2020): Alger. j. biosciences (Dec 2020)
Section
Articles
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

References

Begin J.F. Analyse MCMC de certains modèles de diffusion avec application à la marche Européenne du carbone. Rapport Technique, Université de Montréal, Canada, 2010.

Chib S., Greenberg E. Understanding the Metropolis-Hastings algorithm. The American Statistician.1995, 49, 327–335. DOI: https://doi.org/10.1080/00031305.1995.10476177

Hastings W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970, 57, 97-109. DOI: https://doi.org/10.1093/biomet/57.1.97

Held U. Représentation graphique et comparaison de courbes de survie. Forum Med Suisse.2010, 10(33),548-550. DOI: https://doi.org/10.4414/fms.2010.07252

Khizanov V.G., Maĭboroda R.A modified Kaplan-Meier estimator for a model of mixtures with varying concentrations. Theor. Probability and Math. Statist. 92 (2016), 109-116. DOI: https://doi.org/10.1090/tpms/986

Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H. Equation of state calculations by fast computing machines. The Journal of Chemical Physics. 1953, 21, 1087-1092. DOI: https://doi.org/10.1063/1.1699114

Robert C.P. Le choix Bayésien : principes et pratiques. Springer. 2006.

Rossa A. and Zielinski R. Locally Weibull-Smoothed Kaplan–Meier Estimator, Institute of Mathematics Polish Academy of Sciences, Preprint 599. 1999.

Rossa A., & Zieliński R. A simple improvement of the Kaplan-Meier estimator. Communications in Statistics-Theory and Methods. 2002, 31(1), 147-158. DOI: https://doi.org/10.1081/STA-120002440

Shafiq M., Shah S., & Alamgir M. Modified Weighted Kaplan Meier Estimator. Pakistan Journal of Statistics and Operation Research. 2007, 3(1), 39-44. DOI: https://doi.org/10.18187/pjsor.v3i1.75