Numerical simulation of time-fractional Navier-Stokes equation in cylindrical coordinates for an unsteady one-dimensional motion of a viscous fluid flow in a given tube

Kazeem Iyanda Falade; Adesina Kamorudeen Adio; Omotayo Adebayo Taiwo; Muhammad Auwal Lawan; Sahura Muhammad Badamasi

doi:10.57056/ajet.v8i1.93

Authors

Kazeem Iyanda Falade Department of Mathematics, Faculty of Computing and Mathematical Sciences, Aliko Dangote University of Science and Technology, Wudil, P.M.B 3244, Kano State Nigeria.
Adesina Kamorudeen Adio Department of Basic Sciences, School of Science and Technology, Babcock University, Ilisan-Remo, Ogun State Nigeria.
Omotayo Adebayo Taiwo Department of Physical Science, Mathematics Programme, College of Applied and Physical Sciences, Landmark University, Omu-Aran, Kwara State Nigeria.
Muhammad Auwal Lawan Department of Mathematics, Faculty of Computing and Mathematical Sciences, Aliko Dangote University of Science and Technology, Wudil, P.M.B 3244, Kano State Nigeria.
Sahura Muhammad Badamasi Department of Mathematics, Faculty of Computing and Mathematical Sciences, Aliko Dangote University of Science and Technology, Wudil, P.M.B 3244, Kano State Nigeria.

DOI:

https://doi.org/10.57056/ajet.v8i1.93

Keywords:

Time-fractional Navier-Stokes equation, Cylindrical coordinates, A three-step computational algorithm, Simulation results, 2D and 3D surface plots

Abstract

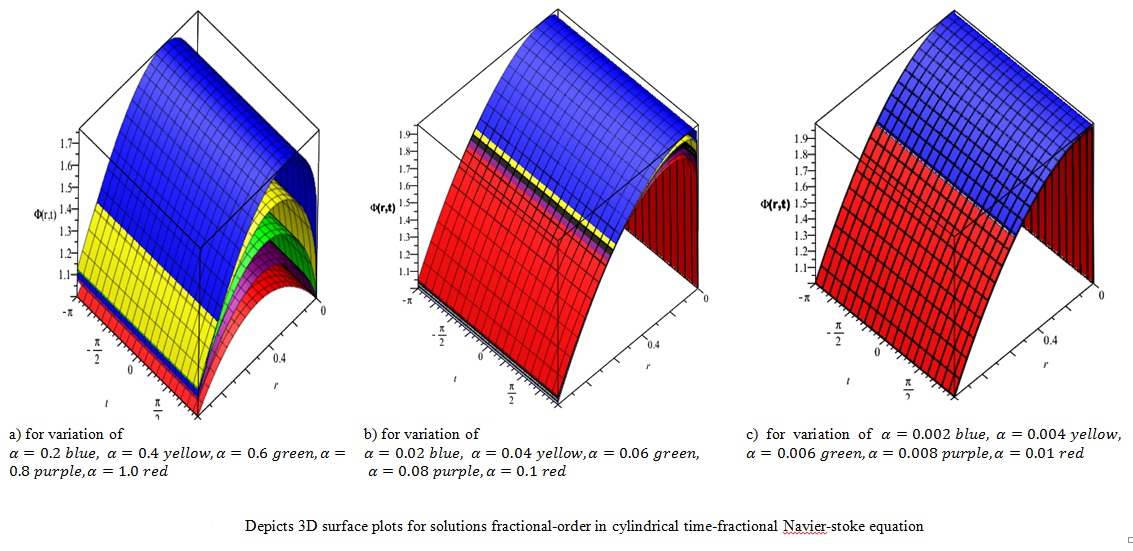
This paper proposed and applied a three-step computational algorithm to solve the time-fractional Navier-Stokes equation (FNS) in a given cylindrical coordinates for one-way unstable flow motion. The Caputo definition of fraction order was obtained using the Riemann Liouville fractional integral operator, which was coded with the MAPLE18 software command and applied to simulate the different fractional values presented in 2D and 3D surface graphs for understanding better the operation of fractional Navier-Stokes equations over time in cylindrical coordinates. We considered different test cases to show the proposed algorithm's efficiency, robustness, and feasibility, which ultimately reduces the computational time and ease of implementation for the simulation of the fractional order of the fractional Navier-Stokes equation considered.

References

Xu L, Chu YM, Rashid S, El-Deeb AA, Nisar KS. On new unified bounds for a family of functions via fractional q-calculus theory. Journal of Function Spaces. 2020;2020:1-9.

Mahmudov NI, Zorlu S. On the approximate controllability of fractional evolution equations with compact analytic semigroup. Journal of Computational and Applied Mathematics. 2014;259:194-204.

Gorenflo R, Mainardi F. Fractional calculus, in Fractals and fractional calculus in continuum mechanics, 1997; 223–276.

Guendouz C, Lazreg JE, Nieto JJ, Ouahab A. Existence and compactness results for a system of fractional differential equations. Journal of Function Spaces. 2020;2020:1-2.

Sabatier JA, Agrawal OP, Machado JT. Advances in fractional calculus, Springer, Dordrecht, Netherlands, 2007.

Falade KI, Tiamiyu AT, Adio AK, Tahir HM, Abubakar UM, Badamasi SM. Computational Relationship of the Surface Area and Stiffness of the Spring Constant on Fractional Bagley-Torvik Equation. Turkish Journal of Science and Technology. 2023;18(1):23-31.

Falade KI, Adio AK, Nuru M, Raifu SA, Muhammad A. Analytical Approximate Solutions of Nonlinear Fractional-Order Nonhomogeneous Differential Equations. Diyala Journal of Engineering Sciences. 2022; 1:94-105.

Manale JM. Group classification of the two-dimensional Navier–Stokes-type equations. International journal of non-linear mechanics. 2000;35(4):627-644.

Girault V, Raviart P. Finite Element Methods for Navier-Stokes Equations, Theory and Algorithms, vol. 5 of Springer Series in Computational Mathematics, Springer, Berlin, Germany, 1986.

Momani S, Odibat Z. Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Applied Mathematics and Computation. 2006;177(2):488-494.

Ragab AA, Hemida KM, Mohamed MS, Abd El Salam MA. Solution of time-fractional Navier–Stokes equation by using homotopy analysis method. Gen. Math. Notes. 2012;13(2):13-21.

Kumar S, Kumar D, Abbasbandy S, Rashidi MM. Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Engineering Journal. 2014;5(2):569-74.

El-Shahed M, Salem A. On the generalized Navier–Stokes equations. Applied Mathematics and Computation. 2004;156(1):287-293.

Ganji ZZ, Ganji DD, Ganji AD, Rostamian M. Analytical solution of time‐fractional Navier–Stokes equation in polar coordinate by homotopy perturbation method. Numerical Methods for Partial Differential Equations: An International Journal. 2010;26(1):117-124.

Singh BK, Kumar P. FRDTM for numerical simulation of multi-dimensional, time-fractional model of Navier–Stokes equation. Ain Shams Engineering Journal. 2018 Dec 1;9(4):827-834.

Jaber KK, Ahmad RS. Analytical solution of the time fractional Navier-Stokes equation. Ain Shams Engineering Journal. 2018;9(4):1917-1927.

Zhang J, Wang J. Numerical analysis for Navier–Stokes equations with time fractional derivatives. Applied Mathematics and Computation. 2018;336:481-489.

Kumar D, Singh J, Kumar S. A fractional model of Navier–Stokes equation arising in unsteady flow of a viscous fluid. Journal of the Association of Arab Universities for Basic and Applied Sciences. 2015;17:14-19.

Jena RM, Chakraverty S. Solving time-fractional Navier–Stokes equations using homotopy perturbation Elzaki transform. SN Applied Sciences. 2019;1:1-3.

Prakash A, Veeresha P, Prakasha DG, Goyal M. A new efficient technique for solving fractional coupled Navier–Stokes equations using q-homotopy analysis transform method. Pramana. 2019;93:1-6.

Zhou Y, Peng L. On the time-fractional Navier-Stokes equations. Computers & Mathematics with Applications.2017;73:874–891.

de Carvalho-Neto PM, Planas G. Mild solutions to the time fractional Navier–Stokes equations in RN. Journal of Differential Equations. 2015;259(7):2948-2980.

Navier CL. Mémoire sur les lois du mouvement des fluides. Mémoires de l’Académie Royale des Sciences de l’Institut de France. 1823;6(1823):389-440.

Wang K, Liu S. Analytical study of time-fractional Navier-Stokes equation by using transform methods. Advances in Difference Equations. 2016;2016:1-12.

Kumar D, Singh J, Kumar S. A fractional model of Navier–Stokes equation arising in unsteady flow of a viscous fluid. Journal of the Association of Arab Universities for Basic and Applied Sciences. 2015;17:14-19.

Kumar S, Kumar D, Abbasbandy S, Rashidi MM. Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Engineering Journal. 2014;5(2):569-574.

Podlubny I. Fractional Differential Equations, Academic Press, 1999; 234-251.